Journal
Ce journal contient 4 entrées.
RSS Feed
Tag cloud
http://www.alanzucconi.com/2015/09/30/colour-sorting/
Le problème de tri des couleurs est directement défini par la difficulté de trouver une relation d'ordre qui soit visuellement satisfaisante pour un espace colorimétrique.
Si l'on prend les nuanciers types arc en ciel, ceux ci sont produits dans un espace HSL en faisant varier la teinte (hue) et en conservant la saturation et la luminance à une valeur fixe (typiquement 1). Essayez sur directement sur http://google.github.io/palette.js
Ici, la relation d'ordre est spécifiée par la valeur de teinte (unidimensionnelle) d'où un bel arc en ciel visuellement uniforme, comme ici : http://www.play-crafts.com/blog/wp-content/uploads/2013/12/hue.jpg
Cependant, si l'on fait varier aléatoirement la teinte, la saturation et la luminance, le bel arc en ciel n'est plus possible car un même vert peut exister en plusieurs niveaux de saturation/luminosité. Avec une simple relation d'ordre lexicographique sur les valeurs de teinte, saturation et luminance, le tri produit ceci http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_hls.png
On observe que l'arc en ciel est là, mais avec des rais de différentes saturation/luminosité qui produisent du bruit dans le résultat.
Si l'on cherche à regrouper les couleurs entre elles, cela peut se faire en divisant l'espace en classes, soit uniformément (découpage en blocs uniformes), soit au moyen d'un algorithme de clustering.
Cela donne un résultat où les couleurs sont effectivement regroupées mais sans arc en ciel global : http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_hsv-lum.png
Il est possible aussi de minimiser la distance entre toutes les couleurs lors de la réduction en dimension 1, ce qui se formalise en problème de voyageur du commerce. Toutefois, si le résultat obtenu est très lisse, il est aussi visuellement aléatoire : http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_nn_hsv.png
dim. 04 oct. 2015 18:01:09 CEST -
-
link
- http://www.alanzucconi.com/2015/09/30/colour-sorting/
colorimétrie
Si l'on prend les nuanciers types arc en ciel, ceux ci sont produits dans un espace HSL en faisant varier la teinte (hue) et en conservant la saturation et la luminance à une valeur fixe (typiquement 1). Essayez sur directement sur http://google.github.io/palette.js
Ici, la relation d'ordre est spécifiée par la valeur de teinte (unidimensionnelle) d'où un bel arc en ciel visuellement uniforme, comme ici : http://www.play-crafts.com/blog/wp-content/uploads/2013/12/hue.jpg
Cependant, si l'on fait varier aléatoirement la teinte, la saturation et la luminance, le bel arc en ciel n'est plus possible car un même vert peut exister en plusieurs niveaux de saturation/luminosité. Avec une simple relation d'ordre lexicographique sur les valeurs de teinte, saturation et luminance, le tri produit ceci http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_hls.png
On observe que l'arc en ciel est là, mais avec des rais de différentes saturation/luminosité qui produisent du bruit dans le résultat.
Si l'on cherche à regrouper les couleurs entre elles, cela peut se faire en divisant l'espace en classes, soit uniformément (découpage en blocs uniformes), soit au moyen d'un algorithme de clustering.
Cela donne un résultat où les couleurs sont effectivement regroupées mais sans arc en ciel global : http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_hsv-lum.png
Il est possible aussi de minimiser la distance entre toutes les couleurs lors de la réduction en dimension 1, ce qui se formalise en problème de voyageur du commerce. Toutefois, si le résultat obtenu est très lisse, il est aussi visuellement aléatoire : http://www.alanzucconi.com/wp-content/uploads/2015/09/sort_nn_hsv.png
dim. 04 oct. 2015 18:01:09 CEST -
-
link
- http://www.alanzucconi.com/2015/09/30/colour-sorting/
colorimétrie
Great Algorithms that Revolutionized Computing
Une petite liste de concepts et d'algorithmes qui ont eu un impact fort sur l'informatique en général, tout particulièrement :
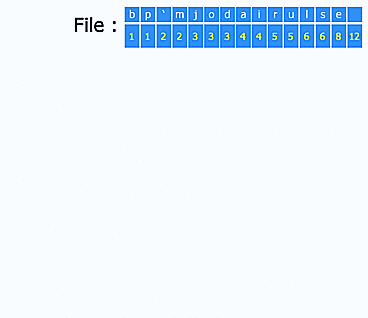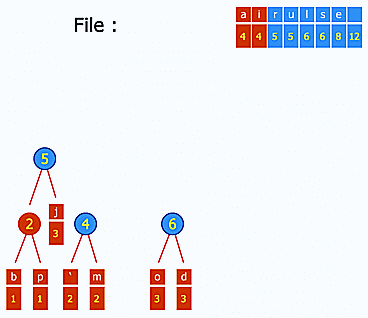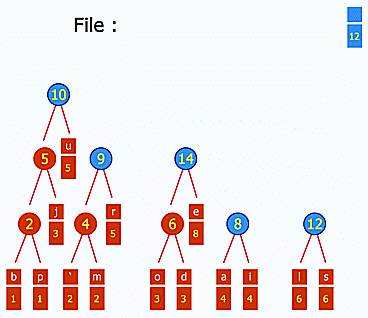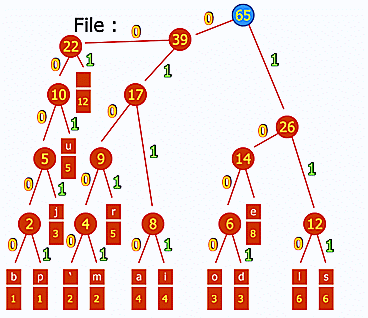
- le codage Huffman pour la compression (ce gif est génial d'ailleurs : http://upload.wikimedia.org/wikipedia/commons/a/ac/Huffman_huff_demo.gif) ;
- le chiffrement à clé publique ;
- l'algorithme de Djikstra pour la recherche des plus courts chemins (applications variées comme, par exemple, le routage) ;
- la recherche dichotomique (binary search) pour trouver un élément dans un tableau trié ;
- le tri rapide (quick sort).
Le choix de ces algorithmes en particulier est arbitraire, de nombreux autres pourraient être cités. Il faudra que je m'y emploie un jour :)
jeu. 10 juil. 2014 10:25:06 CEST -
-
link
- http://en.docsity.com/news/interesting-facts/great-algorithms-revolutionized-computing/
informatique algorithmique compression tri cryptographie
- le codage Huffman pour la compression (ce gif est génial d'ailleurs : http://upload.wikimedia.org/wikipedia/commons/a/ac/Huffman_huff_demo.gif) ;
- le chiffrement à clé publique ;
- l'algorithme de Djikstra pour la recherche des plus courts chemins (applications variées comme, par exemple, le routage) ;
- la recherche dichotomique (binary search) pour trouver un élément dans un tableau trié ;
- le tri rapide (quick sort).
Le choix de ces algorithmes en particulier est arbitraire, de nombreux autres pourraient être cités. Il faudra que je m'y emploie un jour :)
jeu. 10 juil. 2014 10:25:06 CEST -
-
link
- http://en.docsity.com/news/interesting-facts/great-algorithms-revolutionized-computing/
informatique algorithmique compression tri cryptographie
15 Sorting Algorithms in 6 Minutes
Une vidéo pour visualiser comment les algorithmes de tri opèrent sur des ensembles de données aléatoires.
Pour la partie sonore, voir http://panthema.net/2013/sound-of-sorting
EDIT: Dans le même genre, mais en plus bizarre, il y a aussi les algorithmes de tri illustrés par des danses folkloriques : https://www.youtube.com/user/AlgoRythmics/videos
mar. 21 mai 2013 21:19:47 CEST -
-
link
- http://www.youtube.com/watch?v=kPRA0W1kECg
algorithmique tri
Pour la partie sonore, voir http://panthema.net/2013/sound-of-sorting
EDIT: Dans le même genre, mais en plus bizarre, il y a aussi les algorithmes de tri illustrés par des danses folkloriques : https://www.youtube.com/user/AlgoRythmics/videos
mar. 21 mai 2013 21:19:47 CEST -
-
link
- http://www.youtube.com/watch?v=kPRA0W1kECg
algorithmique tri
Principles of Distributed Computing
Un tour d'horizon des principes de l'informatique distribuée. Complet et facile à lire.
jeu. 30 août 2012 21:41:14 CEST -
-
link
- http://disco.ethz.ch/lectures/podc_allstars/
algorithmique systèmes-distribués
jeu. 30 août 2012 21:41:14 CEST -
-
link
- http://disco.ethz.ch/lectures/podc_allstars/
algorithmique systèmes-distribués
Ce journal est basé sur Ginger, un gestionnaire de lien minimaliste développé dans le cadre d'un stage de perfectionnement. Pour plus d'informations, consulter le wiki consacré à mes projets personnels.