Journal
Ce journal contient 29 entrées.

Les algorithmes : nouvelles formes de bureaucraties ? | InternetActu
 L'essayiste Adam Clair dresse une intéressante comparaison entre algorithme et bureaucratie. Les algorithmes sont paradoxaux rappelle-t-il : « ils sont conçus pour améliorer la prise de décision humaine en supprimant supposément ses biais et ses limites, mais les protocoles analytiques inévitablement réducteurs qu’ils mettent en œuvre se révèlent surtout vulnérables à des formes d’utilisation abusive. » Comme le dit très bien Cathy O’Neil dans son livre : loin d’être neutres et objectifs, « les algorithmes sont des opinions formalisées dans du code ».
L'essayiste Adam Clair dresse une intéressante comparaison entre algorithme et bureaucratie. Les algorithmes sont paradoxaux rappelle-t-il : « ils sont conçus pour améliorer la prise de décision humaine en supprimant supposément ses biais et ses limites, mais les protocoles analytiques inévitablement réducteurs qu’ils mettent en œuvre se révèlent surtout vulnérables à des formes d’utilisation abusive. » Comme le dit très bien Cathy O’Neil dans son livre : loin d’être neutres et objectifs, « les algorithmes sont des opinions formalisées dans du code ».
On parle bien sur ici des algorithmes dans le sens restreint de prise de décision pour le compte d'une organisation (les États, en l'occurrence). Par définition, donc, les algorithmes ne sont pas une *nouvelle* forme de bureaucratie ; ils en sont une parfaite implémentation. Il est effectivement peu pertinent de s'en prendre aux algorithmes pour critiquer les travers des bureaucratie, tout comme il est peut pertinent de s'en prendre au machine pour critiquer la disparition de l'emploi.

On parle bien sur ici des algorithmes dans le sens restreint de prise de décision pour le compte d'une organisation (les États, en l'occurrence). Par définition, donc, les algorithmes ne sont pas une *nouvelle* forme de bureaucratie ; ils en sont une parfaite implémentation. Il est effectivement peu pertinent de s'en prendre aux algorithmes pour critiquer les travers des bureaucratie, tout comme il est peut pertinent de s'en prendre au machine pour critiquer la disparition de l'emploi.
Amit’s A* Pages
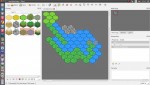 Beaucoup d'informations et d'expérimentations autour de A* (algorithme de pathfinding dont j'avais déjà parlé là en citant le même blog : http://www.benjaminbillet.fr/news/index.php?link=d5gw4e).
Beaucoup d'informations et d'expérimentations autour de A* (algorithme de pathfinding dont j'avais déjà parlé là en citant le même blog : http://www.benjaminbillet.fr/news/index.php?link=d5gw4e).
Il y a plusieurs sujets abordés en bas de page, dont la construction de maps dans les jeux vidéos.
Voir aussi: http://www.redblobgames.com

Il y a plusieurs sujets abordés en bas de page, dont la construction de maps dans les jeux vidéos.
Voir aussi: http://www.redblobgames.com
GitHub - tdebatty/java-string-similarity: Implementation of various string similarity and distance algorithms: Levenshtein, Jaro-winkler, n-Gram, Q-Gr
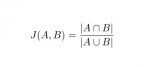 Une librairie Java pour calculer des distances ou des scores de similarité entre des chaînes de caractères.
Une librairie Java pour calculer des distances ou des scores de similarité entre des chaînes de caractères.
Algorithmes implémentés :
Levenshtein O(m*n)
Normalized Levenshtein O(m*n)
Weighted Levenshtein O(m*n)
Damerau-Levenshtein O(m*n)
Optimal String Alignment O(m*n)
Jaro-Winkler O(m*n)
Longest Common Subsequence O(m*n)
Metric Longest Common Subsequence O(m*n)
N-Gram O(m*n)
Q-Gram O(m+n)
Cosine similarity O(m+n)
Jaccard index O(m+n)
Sorensen-Dice coefficient O(m+n)
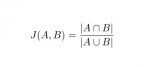
Algorithmes implémentés :
Levenshtein O(m*n)
Normalized Levenshtein O(m*n)
Weighted Levenshtein O(m*n)
Damerau-Levenshtein O(m*n)
Optimal String Alignment O(m*n)
Jaro-Winkler O(m*n)
Longest Common Subsequence O(m*n)
Metric Longest Common Subsequence O(m*n)
N-Gram O(m*n)
Q-Gram O(m+n)
Cosine similarity O(m+n)
Jaccard index O(m+n)
Sorensen-Dice coefficient O(m+n)
Convolution Matrix
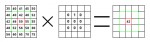 La puissance des matrices de convolution, ou comment créer un filtre de flou, de netteté ou d'estampage avec le même algorithme.
La puissance des matrices de convolution, ou comment créer un filtre de flou, de netteté ou d'estampage avec le même algorithme.

Linear Programming: Introduction
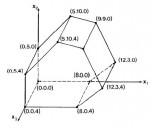 Une introduction aux problèmes d'optimisation linéaire, c'est-à-dire des problème d'optimisation dont la fonction objectif ainsi que les contraintes sont décrites sous la forme de fonctions linéaires.
Une introduction aux problèmes d'optimisation linéaire, c'est-à-dire des problème d'optimisation dont la fonction objectif ainsi que les contraintes sont décrites sous la forme de fonctions linéaires.
Il existe aussi certaines formes, où les variables de décision ne peuvent prendre que des valeurs entières ou binaires. Ces dernières sont connues pour être très difficile à résoudre.
Voir aussi le livre "Practical Optimization: A Gentle Introduction" que l'on peut trouver gratuitement sur le site de l'auteur.
http://www.sce.carleton.ca/faculty/chinneck/po/

Il existe aussi certaines formes, où les variables de décision ne peuvent prendre que des valeurs entières ou binaires. Ces dernières sont connues pour être très difficile à résoudre.
Voir aussi le livre "Practical Optimization: A Gentle Introduction" que l'on peut trouver gratuitement sur le site de l'auteur.
http://www.sce.carleton.ca/faculty/chinneck/po/
Animated Algorithms
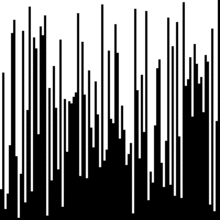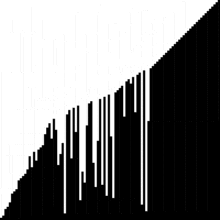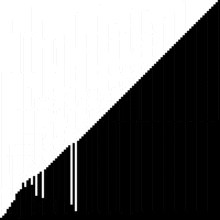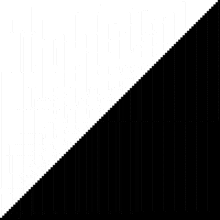 Très classe cet outil de visualisation d'algorithmes. Par exemple :
Très classe cet outil de visualisation d'algorithmes. Par exemple :
http://www.algomation.com/algorithm/heap-sort-priority-queue
http://www.algomation.com/algorithm/prim-minimum-spanning-tree
Et on peut écrire ses propres algos, en javascript.

http://www.algomation.com/algorithm/heap-sort-priority-queue
http://www.algomation.com/algorithm/prim-minimum-spanning-tree
Et on peut écrire ses propres algos, en javascript.
History of Lossless Data Compression Algorithms - GHN: IEEE Global History Network
 Un historique complet des algorithmes de compression sans perte : DEFLATE, LZMA, bzip2, etc.
Un historique complet des algorithmes de compression sans perte : DEFLATE, LZMA, bzip2, etc.
C'est assez concis, facile à comprendre (avec les références qui vont bien pour pouvoir aller creuser en détail telle ou telle technique) et ça balaye aussi bien les méthodes de compression (Huffman, RLE, codage arithmétique, etc.) que les différentes familles d'algorithmes qui en sont issues (algorithmes à fenêtre glissante, à dictionnaire, etc.).

C'est assez concis, facile à comprendre (avec les références qui vont bien pour pouvoir aller creuser en détail telle ou telle technique) et ça balaye aussi bien les méthodes de compression (Huffman, RLE, codage arithmétique, etc.) que les différentes familles d'algorithmes qui en sont issues (algorithmes à fenêtre glissante, à dictionnaire, etc.).
Introduction to A*
 L'algorithme A* (prononcer "a star") est sans doute l'algorithme de pathfinding le plus connu et le plus simple.
L'algorithme A* (prononcer "a star") est sans doute l'algorithme de pathfinding le plus connu et le plus simple.
Celui-ci est expliqué en détail sur cette page, ainsi que l'algorithme de Djikstra et l'algorithme Greedy BFS qui sont combinés dans l'approche A*.

Celui-ci est expliqué en détail sur cette page, ainsi que l'algorithme de Djikstra et l'algorithme Greedy BFS qui sont combinés dans l'approche A*.
List of Free Learning Resources - vhf/free-programming-books - GitHub
 Histoire de ne plus dormir pendant quelques mois, ce repository héberge une très longue liste de livres de programmation, en libre accès. On y trouve aussi des livres portant sur l'algorithmique, des méthodologie de développement, les bases de données, le data mining, les mathématiques, etc.
Histoire de ne plus dormir pendant quelques mois, ce repository héberge une très longue liste de livres de programmation, en libre accès. On y trouve aussi des livres portant sur l'algorithmique, des méthodologie de développement, les bases de données, le data mining, les mathématiques, etc.
Les listes sont organisées par langue (plus de 20 langues) puis par langage ou domaine.
La liste anglaise est vraiment impressionnante :
https://github.com/vhf/free-programming-books/blob/master/free-programming-books.md

Les listes sont organisées par langue (plus de 20 langues) puis par langage ou domaine.
La liste anglaise est vraiment impressionnante :
https://github.com/vhf/free-programming-books/blob/master/free-programming-books.md
Great Algorithms that Revolutionized Computing
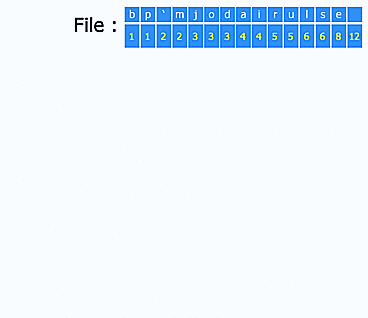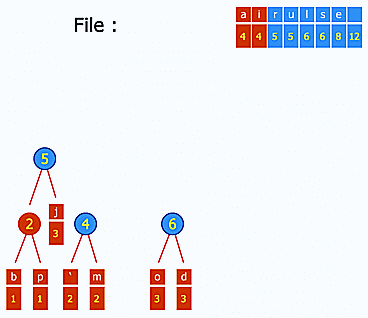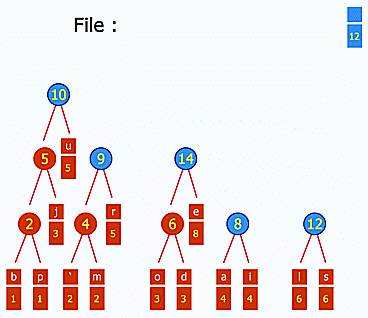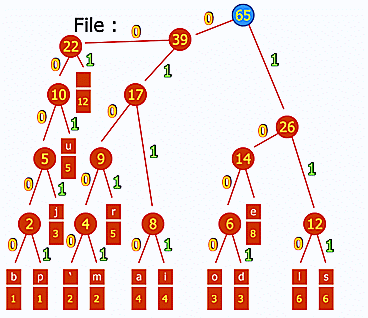 Une petite liste de concepts et d'algorithmes qui ont eu un impact fort sur l'informatique en général, tout particulièrement :
Une petite liste de concepts et d'algorithmes qui ont eu un impact fort sur l'informatique en général, tout particulièrement :
- le codage Huffman pour la compression (ce gif est génial d'ailleurs : http://upload.wikimedia.org/wikipedia/commons/a/ac/Huffman_huff_demo.gif) ;
- le chiffrement à clé publique ;
- l'algorithme de Djikstra pour la recherche des plus courts chemins (applications variées comme, par exemple, le routage) ;
- la recherche dichotomique (binary search) pour trouver un élément dans un tableau trié ;
- le tri rapide (quick sort).
Le choix de ces algorithmes en particulier est arbitraire, de nombreux autres pourraient être cités. Il faudra que je m'y emploie un jour :)

- le codage Huffman pour la compression (ce gif est génial d'ailleurs : http://upload.wikimedia.org/wikipedia/commons/a/ac/Huffman_huff_demo.gif) ;
- le chiffrement à clé publique ;
- l'algorithme de Djikstra pour la recherche des plus courts chemins (applications variées comme, par exemple, le routage) ;
- la recherche dichotomique (binary search) pour trouver un élément dans un tableau trié ;
- le tri rapide (quick sort).
Le choix de ces algorithmes en particulier est arbitraire, de nombreux autres pourraient être cités. Il faudra que je m'y emploie un jour :)
mrb: Types Are The Truth
Pour ceux qui ne comprennent pas le principe de "type erasure", ou qui veulent en apprendre plus à ce sujet.
"Most compilers for full-scale programming languages actually avoid carrying annotations at run time: they are used during typechecking (and during code generation, in more sophisticated compilers), but do not appear in the compiled form of the program."
"Most compilers for full-scale programming languages actually avoid carrying annotations at run time: they are used during typechecking (and during code generation, in more sophisticated compilers), but do not appear in the compiled form of the program."
Gossip Algorithms (2008)
 Un bon livre sur les algorithmes de "gossiping" (gossip = rumeur), qui servent à propager des messages dans les réseaux pair-à-pair mobiles par exemple.
Un bon livre sur les algorithmes de "gossiping" (gossip = rumeur), qui servent à propager des messages dans les réseaux pair-à-pair mobiles par exemple.
Ces types de réseaux sont des ensembles non structurés de machines disposant d'une ou de plusieurs liaisons sans fil, et qui communiquent entre elles de manière opportuniste lorsqu'elles sont à proximité. La structure du réseau (routes, propagation des messages, etc.) émerge alors au fur et à mesure des interactions.
Evidemment, de nouveaux problèmes apparaissent avec ce type de réseaux : problèmes de routage, mobilité, communication sporadique, etc.
D'où le grand nombre de techniques et d'algorithmes spécifiques à ces réseaux.
Le livre est en accès libre, mais je fais une sauvegarde ici :
http://benjaminbillet.fr/media/gossipbook.pdf

Ces types de réseaux sont des ensembles non structurés de machines disposant d'une ou de plusieurs liaisons sans fil, et qui communiquent entre elles de manière opportuniste lorsqu'elles sont à proximité. La structure du réseau (routes, propagation des messages, etc.) émerge alors au fur et à mesure des interactions.
Evidemment, de nouveaux problèmes apparaissent avec ce type de réseaux : problèmes de routage, mobilité, communication sporadique, etc.
D'où le grand nombre de techniques et d'algorithmes spécifiques à ces réseaux.
Le livre est en accès libre, mais je fais une sauvegarde ici :
http://benjaminbillet.fr/media/gossipbook.pdf
The Stony Brook Algorithm Repository
 Un site qui recense un grand nombre d'algorithmes et leurs implémentations pour différents langages (C/C++, Java, Python, etc.).
Un site qui recense un grand nombre d'algorithmes et leurs implémentations pour différents langages (C/C++, Java, Python, etc.).
1.1 Data Structures
Dictionaries, Priority Queues, Suffix Trees and Arrays, Graph Data Structures, Set Data Structures, Kd-Trees
1.2 Numerical Problems
Solving Linear Equations, Bandwidth Reduction, Matrix Multiplication, Determinants and Permanents, Constrained and Unconstrained Optimization, Linear Programming, Random Number Generation, Factoring and Primality Testing, Arbitrary Precision Arithmetic, Knapsack Problem, Discrete Fourier Transform
1.3 Combinatorial Problems
Sorting, Searching, Median and Selection, Generating Permutations, Generating Subsets, Generating Partitions, Generating Graphs, Calendrical Calculations, Job Scheduling, Satisfiability
1.4 Graph Problems -polynomial-time problems, Connected Components, Topological Sorting, Minimum Spanning Tree, Shortest Path, Transitive Closure and Reduction, Matching, Eulerian Cycle / Chinese Postman, Edge and Vertex Connectivity, Network Flow, Drawing Graphs Nicely, Drawing Trees, Planarity Detection and Embedding
1.5 Graph Problems -hard problems, Clique, Independent Set, Vertex Cover, Traveling Salesman Problem, Hamiltonian Cycle, Graph Partition, Vertex Coloring, Edge Coloring, Graph Isomorphism, Steiner Tree, Feedback Edge/Vertex Set
1.6 Computational Geometry
Robust Geometric Primitives, Convex Hull, Triangulation, Voronoi Diagrams, Nearest Neighbor Search, Range Search, Point Location, Intersection Detection, Bin Packing, Medial-Axis Transformation, Polygon Partitioning, Simplifying Polygons, Shape Similarity, Motion Planning, Maintaining Line Arrangements, Minkowski Sum
1.7 Set and String Problems
Set Cover, Set Packing, String Matching, Approximate String Matching, Text Compression, Cryptography, Finite State Machine Minimization, Longest Common Substring, - Shortest Common Superstring

1.1 Data Structures
Dictionaries, Priority Queues, Suffix Trees and Arrays, Graph Data Structures, Set Data Structures, Kd-Trees
1.2 Numerical Problems
Solving Linear Equations, Bandwidth Reduction, Matrix Multiplication, Determinants and Permanents, Constrained and Unconstrained Optimization, Linear Programming, Random Number Generation, Factoring and Primality Testing, Arbitrary Precision Arithmetic, Knapsack Problem, Discrete Fourier Transform
1.3 Combinatorial Problems
Sorting, Searching, Median and Selection, Generating Permutations, Generating Subsets, Generating Partitions, Generating Graphs, Calendrical Calculations, Job Scheduling, Satisfiability
1.4 Graph Problems -polynomial-time problems, Connected Components, Topological Sorting, Minimum Spanning Tree, Shortest Path, Transitive Closure and Reduction, Matching, Eulerian Cycle / Chinese Postman, Edge and Vertex Connectivity, Network Flow, Drawing Graphs Nicely, Drawing Trees, Planarity Detection and Embedding
1.5 Graph Problems -hard problems, Clique, Independent Set, Vertex Cover, Traveling Salesman Problem, Hamiltonian Cycle, Graph Partition, Vertex Coloring, Edge Coloring, Graph Isomorphism, Steiner Tree, Feedback Edge/Vertex Set
1.6 Computational Geometry
Robust Geometric Primitives, Convex Hull, Triangulation, Voronoi Diagrams, Nearest Neighbor Search, Range Search, Point Location, Intersection Detection, Bin Packing, Medial-Axis Transformation, Polygon Partitioning, Simplifying Polygons, Shape Similarity, Motion Planning, Maintaining Line Arrangements, Minkowski Sum
1.7 Set and String Problems
Set Cover, Set Packing, String Matching, Approximate String Matching, Text Compression, Cryptography, Finite State Machine Minimization, Longest Common Substring, - Shortest Common Superstring
Mining of Massive Datasets
Un super bouquin sur le data mining, dont la couverture est certes moche, mais dont vous pouvez lire le contenu en ligne.
J'apprécie tout particulièrement son chapitre sur le stream processing, qui me concerne spécifiquement.
J'ai fait un backup du PDF du livre ici : http://benjaminbillet.fr/media/mining-of-massive-datasets.pdf
J'apprécie tout particulièrement son chapitre sur le stream processing, qui me concerne spécifiquement.
J'ai fait un backup du PDF du livre ici : http://benjaminbillet.fr/media/mining-of-massive-datasets.pdf
C'est quoi la récursion terminale ?
Avant toute chose, nous devons parler de la pile d'exécution (ou "pile des appels", ou tout simplement "pile").
La pile d'exécution est un espace de stockage permettant d'enregistrer l'endroit où chaque fonction active (= les fonctions invoquées mais non terminées) doit retourner à la fin de son exécution. Elle enregistre donc des adresses, mais aussi le contexte des fonctions actives (les variables locales, les paramètres, etc.).
Le principe de la pile est le suivant: si une fonction A invoque une fonction B, alors on stocke A au sommet de la pile pour savoir où reprendre lorsque B sera terminée. Si B invoque une fonction C, B sera placé au sommet de la pile à son tour. A la fin de C, on récupère B au sommet de la pile, et à la fin de B on récupère A au sommet de la pile (d'où le terme de pile, car on y empile et on y dépile des éléments).
Alors, imaginons une factorielle naïve :
fact(n)
{
if(n == 1) // cas de base
return 1;
else
return n * fact(n - 1);
}
Décomposons notre fonction fact : pour calculer n * fact(n - 1), il est évidemment nécessaire de calculer fact(n - 1). Cela implique que fact(n) ne peut pas retourner de résultat sans d'abord obtenir le résultat de fact(n - 1). Avant d'exécuter fact(n - 1), on place donc fact(n) au sommet de la pile et on exécute fact(n - 1).
Sauf qu'évidemment, le problème se pose à nouveau : pour calculer fact(n - 1) on doit tout d'abord calculer fact(n - 2), et on place donc fact(n - 1) sur la pile. Et ainsi de suite jusqu'à ce que l'on atteigne fact(1) qui retourne immédiatement 1.
Le souci c'est que notre pile n'est pas infinie. Dans les langages classiques type C ou Java, elle est même ridiculement petite. Lorsqu'elle est pleine, le programme crashe car il n'est plus possible d'invoquer de nouvelle fonction : c'est le dépassement (ou débordement) de pile, stack overflow en anglais.
Une fonction récursive terminale, c'est tout simplement une fonction récursive particulière, où la récursion ne fait intervenir aucune autre opération que l'appel de la fonction. Ce qui, pour notre factorielle se traduit ainsi :
fact(n, total)
{
if(n == 0)
return total;
else
return fact(n - 1, total * (n - 1));
}
Ici, lorsque l'on arrive fact(n - 1, total * (n - 1)), il n'y a rien à sauvegarder. Il suffit donc simplement de remplacer fact(n, total) par fact(n - 1, total * (n - 1)) au sommet de la pile. L'espace nécessaire sur la pile pour exécuter fact(n, total) est donc constant, ce qui assure que la pile ne débordera pas, même pour un très grand nombre de récursion.
Hélas, cette optimisation n'est pas implicite et doit être effectuée à la compilation. Beaucoup de langages classiques ne le font pas (Java, C#, Python, C/C++ sauf avec l'option -foptimize-sibling-calls, etc.). Il s'agit donc principalement d'une propriété typique des langages fonctionnels car ceux ci font massivement appel à la récursion.
La pile d'exécution est un espace de stockage permettant d'enregistrer l'endroit où chaque fonction active (= les fonctions invoquées mais non terminées) doit retourner à la fin de son exécution. Elle enregistre donc des adresses, mais aussi le contexte des fonctions actives (les variables locales, les paramètres, etc.).
Le principe de la pile est le suivant: si une fonction A invoque une fonction B, alors on stocke A au sommet de la pile pour savoir où reprendre lorsque B sera terminée. Si B invoque une fonction C, B sera placé au sommet de la pile à son tour. A la fin de C, on récupère B au sommet de la pile, et à la fin de B on récupère A au sommet de la pile (d'où le terme de pile, car on y empile et on y dépile des éléments).
Alors, imaginons une factorielle naïve :
fact(n)
{
if(n == 1) // cas de base
return 1;
else
return n * fact(n - 1);
}
Décomposons notre fonction fact : pour calculer n * fact(n - 1), il est évidemment nécessaire de calculer fact(n - 1). Cela implique que fact(n) ne peut pas retourner de résultat sans d'abord obtenir le résultat de fact(n - 1). Avant d'exécuter fact(n - 1), on place donc fact(n) au sommet de la pile et on exécute fact(n - 1).
Sauf qu'évidemment, le problème se pose à nouveau : pour calculer fact(n - 1) on doit tout d'abord calculer fact(n - 2), et on place donc fact(n - 1) sur la pile. Et ainsi de suite jusqu'à ce que l'on atteigne fact(1) qui retourne immédiatement 1.
Le souci c'est que notre pile n'est pas infinie. Dans les langages classiques type C ou Java, elle est même ridiculement petite. Lorsqu'elle est pleine, le programme crashe car il n'est plus possible d'invoquer de nouvelle fonction : c'est le dépassement (ou débordement) de pile, stack overflow en anglais.
Une fonction récursive terminale, c'est tout simplement une fonction récursive particulière, où la récursion ne fait intervenir aucune autre opération que l'appel de la fonction. Ce qui, pour notre factorielle se traduit ainsi :
fact(n, total)
{
if(n == 0)
return total;
else
return fact(n - 1, total * (n - 1));
}
Ici, lorsque l'on arrive fact(n - 1, total * (n - 1)), il n'y a rien à sauvegarder. Il suffit donc simplement de remplacer fact(n, total) par fact(n - 1, total * (n - 1)) au sommet de la pile. L'espace nécessaire sur la pile pour exécuter fact(n, total) est donc constant, ce qui assure que la pile ne débordera pas, même pour un très grand nombre de récursion.
Hélas, cette optimisation n'est pas implicite et doit être effectuée à la compilation. Beaucoup de langages classiques ne le font pas (Java, C#, Python, C/C++ sauf avec l'option -foptimize-sibling-calls, etc.). Il s'agit donc principalement d'une propriété typique des langages fonctionnels car ceux ci font massivement appel à la récursion.
The Balancing Act of Choosing Nonblocking Features - ACM Queue
 Je vous ai déjà rapidement parlé de l'avantage des algorithmes sans verrous (lock-free) : http://benjaminbillet.fr/news/index.php?link=d5gw1q
Je vous ai déjà rapidement parlé de l'avantage des algorithmes sans verrous (lock-free) : http://benjaminbillet.fr/news/index.php?link=d5gw1q
Cet article revient en détails sur les différentes techniques et sur la difficulté de choisir des algorithmes et des structures de données lock-free pour un contexte donné.
Une sauvegarde de l'article en PDF ici :
http://benjaminbillet.fr/media/balancing-act-choosing-nonblocking-features.pdf

Cet article revient en détails sur les différentes techniques et sur la difficulté de choisir des algorithmes et des structures de données lock-free pour un contexte donné.
Une sauvegarde de l'article en PDF ici :
http://benjaminbillet.fr/media/balancing-act-choosing-nonblocking-features.pdf
Bloom filter
Un filtre de Bloom est une structure de données probabiliste qui permet de tester si un élément appartient à un ensemble.
Une telle structure est plus compacte (taille fixe) que l'ensemble lui même, et peut permettre de savoir avec certitude qu'un élément est absent de l'ensemble. Cependant, il existe une probabilité donnée d'obtenir des faux positifs lorsque l'on teste si un élément est présent dans l'ensemble.
EDIT : un exemple en python ici http://www.stavros.io/posts/bloom-filter-search-engine/?print
Une telle structure est plus compacte (taille fixe) que l'ensemble lui même, et peut permettre de savoir avec certitude qu'un élément est absent de l'ensemble. Cependant, il existe une probabilité donnée d'obtenir des faux positifs lorsque l'on teste si un élément est présent dans l'ensemble.
EDIT : un exemple en python ici http://www.stavros.io/posts/bloom-filter-search-engine/?print
Problem Solving with Algorithms and Data Structures
 Un livre en ligne, qui balaye un certains nombres algorithmes (parcours, tri, etc.) et structure de données (piles, files, listes, graphes, arbres, etc.). Le tout avec des exemples orientés Python.
Un livre en ligne, qui balaye un certains nombres algorithmes (parcours, tri, etc.) et structure de données (piles, files, listes, graphes, arbres, etc.). Le tout avec des exemples orientés Python.

15 Sorting Algorithms in 6 Minutes
 Une vidéo pour visualiser comment les algorithmes de tri opèrent sur des ensembles de données aléatoires.
Une vidéo pour visualiser comment les algorithmes de tri opèrent sur des ensembles de données aléatoires.
Pour la partie sonore, voir http://panthema.net/2013/sound-of-sorting
EDIT: Dans le même genre, mais en plus bizarre, il y a aussi les algorithmes de tri illustrés par des danses folkloriques : https://www.youtube.com/user/AlgoRythmics/videos

Pour la partie sonore, voir http://panthema.net/2013/sound-of-sorting
EDIT: Dans le même genre, mais en plus bizarre, il y a aussi les algorithmes de tri illustrés par des danses folkloriques : https://www.youtube.com/user/AlgoRythmics/videos
Lockfree Algorithms
En général, limiter le nombre de verrous dans un programme multithread est une bonne pratique, pour deux raisons :
1. cela réduit le nombre d'erreurs imprévues (interblocage, verrous inutiles, etc.).
2. cela augmente la cohérence du programme (grosso modo, pourquoi faire des threads si c'est pour ensuite mettre des verrous partout).
Aussi, rien de mieux que les algorithmes sans synchronisation.
1. cela réduit le nombre d'erreurs imprévues (interblocage, verrous inutiles, etc.).
2. cela augmente la cohérence du programme (grosso modo, pourquoi faire des threads si c'est pour ensuite mettre des verrous partout).
Aussi, rien de mieux que les algorithmes sans synchronisation.

Ce journal est basé sur Ginger, un gestionnaire de lien minimaliste développé dans le cadre d'un stage de perfectionnement. Pour plus d'informations, consulter le wiki consacré à mes projets personnels.
 RSS Feed
RSS Feed Tag cloud
Tag cloud sam. 08 avril 2017 18:04:57 CEST
sam. 08 avril 2017 18:04:57 CEST
 société algorithmique
société algorithmique