Journal
Ce journal contient 19 entrées.
RSS Feed
Tag cloud
Seeing Theory
A visual introduction to probability and statistics.
dim. 05 mai 2019 10:42:03 CEST -
-
link
- https://seeing-theory.brown.edu
mathématiques statistiques
dim. 05 mai 2019 10:42:03 CEST -
-
link
- https://seeing-theory.brown.edu
mathématiques statistiques
Computing linear regression in one pass
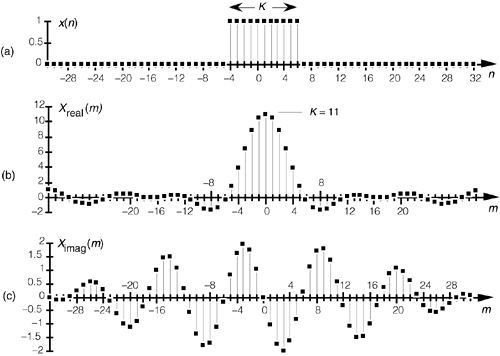
Dans le même ordre d'idée que le lien précédent, sauf qu'il s'agit cette fois d'effectuer une régression linéaire en continu. Comme beaucoup d'algorithmes continu, il présente l'avantage de travailler en mémoire constante.
Le thumbnail vient de XKCD : https://xkcd.com/1725
lun. 10 avril 2017 10:32:57 CEST -
-
link
- https://www.johndcook.com/blog/running_regression/
mathématiques statistiques stream-processing
Le thumbnail vient de XKCD : https://xkcd.com/1725
lun. 10 avril 2017 10:32:57 CEST -
-
link
- https://www.johndcook.com/blog/running_regression/
mathématiques statistiques stream-processing
Computing skewness and kurtosis in one pass
Comme vous l'avez peut être déjà remarqué, une bonne partie de mes travaux de thèse ont porté sur le traitement continu de flux de données : http://benjaminbillet.fr/media/benjaminbillet_memoire.pdf
De fait, je m'intéresse beaucoup aux techniques mathématiques permettant de réaliser des calculs en continu (c'est-à-dire sans mémoriser l'intégralité des résultats passés).
Cet article de blog décrit comment calculer en continu l'espérance, la variance, l'écart-type, le coefficient de dissymétrie et le coefficient d'aplatissement sur un flux d'échantillons. De manière plus générale il s'agit d'une méthode pour calculer les moments (https://fr.wikipedia.org/wiki/Moment_%28mathématiques%29). On pourrait imaginer donc l'utiliser pour calculer d'autres mesures statistiques d'ordre supérieur. J'essayerais d'ailleurs, si je parviens à bien tout comprendre, d'en faire une implémentation généralisée :)
Quelques références:
- B. P. Welford (1962)."Note on a method for calculating corrected sums of squares and products".
- Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn.
lun. 10 avril 2017 10:22:27 CEST -
-
link
- https://www.johndcook.com/blog/skewness_kurtosis/
mathématiques statistiques stream-processing
De fait, je m'intéresse beaucoup aux techniques mathématiques permettant de réaliser des calculs en continu (c'est-à-dire sans mémoriser l'intégralité des résultats passés).
Cet article de blog décrit comment calculer en continu l'espérance, la variance, l'écart-type, le coefficient de dissymétrie et le coefficient d'aplatissement sur un flux d'échantillons. De manière plus générale il s'agit d'une méthode pour calculer les moments (https://fr.wikipedia.org/wiki/Moment_%28mathématiques%29). On pourrait imaginer donc l'utiliser pour calculer d'autres mesures statistiques d'ordre supérieur. J'essayerais d'ailleurs, si je parviens à bien tout comprendre, d'en faire une implémentation généralisée :)
Quelques références:
- B. P. Welford (1962)."Note on a method for calculating corrected sums of squares and products".
- Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn.
lun. 10 avril 2017 10:22:27 CEST -
-
link
- https://www.johndcook.com/blog/skewness_kurtosis/
mathématiques statistiques stream-processing
Séries de Fourier
Voir aussi: http://www.benjaminbillet.fr/news/index.php?link=d5gw8e
mer. 25 janv. 2017 09:10:18 CET -
-
link
- http://licence-eea.fr/series-de-fourier/
mathématiques signal-processing
mer. 25 janv. 2017 09:10:18 CET -
-
link
- http://licence-eea.fr/series-de-fourier/
mathématiques signal-processing
7 techniques mathématiques
1. La descente de gradient
2. Le kdtree
3. La décomposition en valeurs singulières
4. La dimension de Vapnik-chervonenkis
5. Distributed Stochastic Neighboor Embedding
6. Radial basis Kernel trick
7. Affinity Propagation Clustering
lun. 17 oct. 2016 15:16:59 CEST -
-
link
- https://li.st/l/f00d8e06-3e49-4a69-97eb-dc3729b808f5
mathématiques
2. Le kdtree
3. La décomposition en valeurs singulières
4. La dimension de Vapnik-chervonenkis
5. Distributed Stochastic Neighboor Embedding
6. Radial basis Kernel trick
7. Affinity Propagation Clustering
lun. 17 oct. 2016 15:16:59 CEST -
-
link
- https://li.st/l/f00d8e06-3e49-4a69-97eb-dc3729b808f5
mathématiques
Une introduction aux arbres de décision
Résumé :
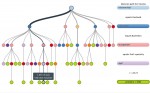
Les arbres de décision sont l’une des structures de données majeures de l’apprentissage statistique. Leur fonctionnement repose sur des heuristiques qui, tout en satisfaisant l’intuition, donnent des résultats remarquables en pratique (notamment lorsqu’ils sont utilisés en « forêts aléatoires »). Leur structure arborescente les rend également lisibles par un être humain, contrairement à d’autres approches où le prédicteur construit est une « boîte noire ».
L’introduction que nous proposons ici décrit les bases de leur fonctionnement tout en apportant quelques justifications théoriques. Nous aborderons aussi (brièvement) l’extension aux Random Forests. On supposera le lecteur familier avec le contexte général de l’apprentissage supervisé.1
lun. 17 oct. 2016 15:10:56 CEST -
-
link
- https://scaron.info/doc/intro-arbres-decision/
machine-learning mathématiques
Les arbres de décision sont l’une des structures de données majeures de l’apprentissage statistique. Leur fonctionnement repose sur des heuristiques qui, tout en satisfaisant l’intuition, donnent des résultats remarquables en pratique (notamment lorsqu’ils sont utilisés en « forêts aléatoires »). Leur structure arborescente les rend également lisibles par un être humain, contrairement à d’autres approches où le prédicteur construit est une « boîte noire ».
L’introduction que nous proposons ici décrit les bases de leur fonctionnement tout en apportant quelques justifications théoriques. Nous aborderons aussi (brièvement) l’extension aux Random Forests. On supposera le lecteur familier avec le contexte général de l’apprentissage supervisé.1
lun. 17 oct. 2016 15:10:56 CEST -
-
link
- https://scaron.info/doc/intro-arbres-decision/
machine-learning mathématiques
How Not To Sort By Average Rating
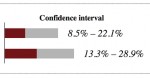Une meilleure méthode pour la gestion des notations. Cette technique prend en compte à la fois la proportion de notes positives et la taille de l'échantillon.
sam. 06 août 2016 15:08:43 CEST -
-
link
- http://www.evanmiller.org/how-not-to-sort-by-average-rating.html
mathématiques
sam. 06 août 2016 15:08:43 CEST -
-
link
- http://www.evanmiller.org/how-not-to-sort-by-average-rating.html
mathématiques
Maths and Science blog- matthen
Des animations de curiosités mathématiques.
dim. 03 avril 2016 10:25:00 CEST -
-
link
- http://blog.matthen.com/
mathématiques animation
dim. 03 avril 2016 10:25:00 CEST -
-
link
- http://blog.matthen.com/
mathématiques animation
Neural networks and deep learning
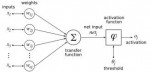Les réseaux neuronaux ont connu une évolution difficile dans le domaine de l'intelligence artificielle (engouement, rejet, engouement, etc.). En très bref, il s'agit de réseaux formés par l'interconnexion d'entités appelées "perceptrons". Ces perceptrons miment grossièrement le fonctionnement d'un neurone en émettant un signal plus ou moins fort en fonction de leurs entrées.
Ils reviennent à la mode sous le nom de "deep learning". Je suis donc en train de lire ce livre en ligne sur le sujet. L'auteur maîtrise son sujet et parvient à l'expliquer (en anglais) dans sa globalité : il rentre de manière très progressive dans la formalisation mathématiques du problème puis dans les différents aspects fondamentaux :
- l'activation du réseau
- la descente de gradient
- l'algorithme de rétropropagation
- la régression softmax
- etc... (je n'ai pas encore fini de lire)
L'auteur utilise le cas de la reconnaissance de caractère comme fil rouge et illustre tout ceci avec des implémentations en Python.
ven. 13 déc. 2013 11:07:31 CET -
-
link
- http://neuralnetworksanddeeplearning.com/chap1.html
mathématiques machine-learning
Ils reviennent à la mode sous le nom de "deep learning". Je suis donc en train de lire ce livre en ligne sur le sujet. L'auteur maîtrise son sujet et parvient à l'expliquer (en anglais) dans sa globalité : il rentre de manière très progressive dans la formalisation mathématiques du problème puis dans les différents aspects fondamentaux :
- l'activation du réseau
- la descente de gradient
- l'algorithme de rétropropagation
- la régression softmax
- etc... (je n'ai pas encore fini de lire)
L'auteur utilise le cas de la reconnaissance de caractère comme fil rouge et illustre tout ceci avec des implémentations en Python.
ven. 13 déc. 2013 11:07:31 CET -
-
link
- http://neuralnetworksanddeeplearning.com/chap1.html
mathématiques machine-learning
How to build an Anti Aircraft Missile: Probability, Bayes’ Theorem and the Kalman Filter
Un article expliquant brièvement le théorème de Bayes et le filtre de Kalman.
http://en.wikipedia.org/wiki/Kalman_filter
jeu. 24 oct. 2013 13:20:51 CEST -
-
link
- http://georgemdallas.wordpress.com/2013/07/13/how-to-build-an-anti-aircraft-missile-probability-bayes-theorem-and-the-kalman-filter/
mathématiques
http://en.wikipedia.org/wiki/Kalman_filter
jeu. 24 oct. 2013 13:20:51 CEST -
-
link
- http://georgemdallas.wordpress.com/2013/07/13/how-to-build-an-anti-aircraft-missile-probability-bayes-theorem-and-the-kalman-filter/
mathématiques
De la place des mathématiques dans la programmation
J'entends souvent les développeurs débutants dire que les mathématiques ne sont pas utiles pour programmer.
En un sens ce n'est pas totalement faux, les mathématiques ne sont pas strictement nécessaires pour écrire des programmes. Toutefois, c'est uniquement car les programmes que nous écrivons font appel à des librairies qui résolvent la plupart des problèmes véritablement complexes que nous pourrions rencontrer. Ces librairies sont des boîtes noires qui nous masquent les détails mathématiques et algorithmiques sous-jacent, mais hélas ce n'est pas parce que nous ne manipulons pas ces détails qu'ils n'existent pas ;)
En fait, on retrouve des fondements mathématiques dans quasiment tous les domaines de l'informatique.
Retrouver des données "intéressantes" dans de grands ensembles (data mining, moteur de recherche) ? Des statistiques, des filtres, etc.
Les bases de données ? Théorie des ensembles, fonctions de hachage, etc.
L'encodage audio/vidéo ? Analyse numérique, mathématiques du signal, DFT, échantillonnage, statistiques, ...
La 3D ? Alors là c'est le pire je pense ; géométrie dans l'espace, physique, calcul vectoriel, calcul matriciel, calcul intégral, espaces, analyse numérique, algèbre, ...
Le chiffrement ? La compression ? La détection des erreurs ? Arithmétique modulaire, théorie des ensembles, théorie de l'information, ...
OCR ? Reconnaissance vocale ? Statistiques, réseaux bayésiens, réseaux de neurones, ...
Les réseaux ? Théorie de l'information, théorie des graphes, statistiques, ...
Ce n'est pas parce que nous ne manipulons pas toutes ces choses au quotidien qu'elles n'existent pas. Les ignorer revient à s'en remettre à des boîtes noires prétendument magiques, et à mal les utiliser.
jeu. 05 sept. 2013 17:13:35 CEST -
-
link
science programmation mathématiques
En un sens ce n'est pas totalement faux, les mathématiques ne sont pas strictement nécessaires pour écrire des programmes. Toutefois, c'est uniquement car les programmes que nous écrivons font appel à des librairies qui résolvent la plupart des problèmes véritablement complexes que nous pourrions rencontrer. Ces librairies sont des boîtes noires qui nous masquent les détails mathématiques et algorithmiques sous-jacent, mais hélas ce n'est pas parce que nous ne manipulons pas ces détails qu'ils n'existent pas ;)
En fait, on retrouve des fondements mathématiques dans quasiment tous les domaines de l'informatique.
Retrouver des données "intéressantes" dans de grands ensembles (data mining, moteur de recherche) ? Des statistiques, des filtres, etc.
Les bases de données ? Théorie des ensembles, fonctions de hachage, etc.
L'encodage audio/vidéo ? Analyse numérique, mathématiques du signal, DFT, échantillonnage, statistiques, ...
La 3D ? Alors là c'est le pire je pense ; géométrie dans l'espace, physique, calcul vectoriel, calcul matriciel, calcul intégral, espaces, analyse numérique, algèbre, ...
Le chiffrement ? La compression ? La détection des erreurs ? Arithmétique modulaire, théorie des ensembles, théorie de l'information, ...
OCR ? Reconnaissance vocale ? Statistiques, réseaux bayésiens, réseaux de neurones, ...
Les réseaux ? Théorie de l'information, théorie des graphes, statistiques, ...
Ce n'est pas parce que nous ne manipulons pas toutes ces choses au quotidien qu'elles n'existent pas. Les ignorer revient à s'en remettre à des boîtes noires prétendument magiques, et à mal les utiliser.
jeu. 05 sept. 2013 17:13:35 CEST -
-
link
science programmation mathématiques
Statistical Formulas For Programmers
Quelques formules propres aux statistiques (intervalle de confiance, test du X², comparer des distribution et déterminer des courbes de tendances), utiles pour les programmeurs.
mer. 17 juil. 2013 17:49:57 CEST -
-
link
- http://www.evanmiller.org/statistical-formulas-for-programmers.html
mathématiques
mer. 17 juil. 2013 17:49:57 CEST -
-
link
- http://www.evanmiller.org/statistical-formulas-for-programmers.html
mathématiques
Bloom filter
Un filtre de Bloom est une structure de données probabiliste qui permet de tester si un élément appartient à un ensemble.
Une telle structure est plus compacte (taille fixe) que l'ensemble lui même, et peut permettre de savoir avec certitude qu'un élément est absent de l'ensemble. Cependant, il existe une probabilité donnée d'obtenir des faux positifs lorsque l'on teste si un élément est présent dans l'ensemble.
EDIT : un exemple en python ici http://www.stavros.io/posts/bloom-filter-search-engine/?print
mar. 16 juil. 2013 11:37:46 CEST -
-
link
- http://en.wikipedia.org/wiki/Bloom_filter
mathématiques algorithmique
Une telle structure est plus compacte (taille fixe) que l'ensemble lui même, et peut permettre de savoir avec certitude qu'un élément est absent de l'ensemble. Cependant, il existe une probabilité donnée d'obtenir des faux positifs lorsque l'on teste si un élément est présent dans l'ensemble.
EDIT : un exemple en python ici http://www.stavros.io/posts/bloom-filter-search-engine/?print
mar. 16 juil. 2013 11:37:46 CEST -
-
link
- http://en.wikipedia.org/wiki/Bloom_filter
mathématiques algorithmique
Formule autoréférente de Tupper - Wikipédia
Lorsque l'on trace l'ensemble des couples (x,y) qui satisfont cette inégalité, une partie du plan représente la formule elle-même.
Description détaillée : http://p3.storage.canalblog.com/36/80/210892/67522113.png
jeu. 06 juin 2013 15:12:06 CEST -
-
link
- https://fr.wikipedia.org/wiki/Formule_autor%C3%A9f%C3%A9rente_de_Tupper
mathématiques curiosité
Description détaillée : http://p3.storage.canalblog.com/36/80/210892/67522113.png
jeu. 06 juin 2013 15:12:06 CEST -
-
link
- https://fr.wikipedia.org/wiki/Formule_autor%C3%A9f%C3%A9rente_de_Tupper
mathématiques curiosité
Functors, Applicatives, And Monads In Pictures
La programmation fonctionnelle emprunte un vocabulaire parfois obscur aux mathématiques, d'où cet intéressant petit article illustré qui revient sur les concepts de "fonctor" (foncteur), "monad" (monoïde) et "applicative" (foncteur applicatif).
Une autre explication, en français :
http://lyah.haskell.fr/foncteurs-foncteurs-applicatifs-et-monoides
mer. 17 avril 2013 18:02:47 CEST -
-
link
- http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html
programmation fonctionnel mathématiques
Une autre explication, en français :
http://lyah.haskell.fr/foncteurs-foncteurs-applicatifs-et-monoides
mer. 17 avril 2013 18:02:47 CEST -
-
link
- http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html
programmation fonctionnel mathématiques
Moyenne glissante
C'est impressionnant le nombre de gens qui travaillent sur les problèmes de stream processing et qui n'ont jamais entendu parler des moyennes glissantes.
C'est une formule très simple pour calculer une moyenne au fur et à mesure que les éléments sont reçus (pas besoin de conserver la somme totale, ce qui atténue les problèmes de débordement lorsque le nombre d'éléments devient très grand).
http://fr.wikipedia.org/wiki/Moyenne#Moyenne_glissante
jeu. 04 avril 2013 11:25:59 CEST -
-
link
- http://fr.wikipedia.org/wiki/Moyenne#Moyenne_glissante
mathématiques
C'est une formule très simple pour calculer une moyenne au fur et à mesure que les éléments sont reçus (pas besoin de conserver la somme totale, ce qui atténue les problèmes de débordement lorsque le nombre d'éléments devient très grand).
http://fr.wikipedia.org/wiki/Moyenne#Moyenne_glissante
jeu. 04 avril 2013 11:25:59 CEST -
-
link
- http://fr.wikipedia.org/wiki/Moyenne#Moyenne_glissante
mathématiques
Equations for Organic Motion
Quelques formules pour reproduire des mouvements "organiques".
ven. 02 nov. 2012 09:32:14 CET -
-
link
- http://codepen.io/soulwire/full/kqHxB
mathématiques curiosité
ven. 02 nov. 2012 09:32:14 CET -
-
link
- http://codepen.io/soulwire/full/kqHxB
mathématiques curiosité
Exotic Data Structures
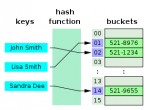Les structures de données, c'est probablement les éléments que l'on manipule le plus sans en avoir conscience, et ce dans n'importe que langage de programmation. Il en existe une quantité phénoménale, reposant souvent sur des fondements algorithmiques et mathématiques complexes.
jeu. 25 oct. 2012 14:42:52 CEST -
-
link
- http://concatenative.org/wiki/view/Exotic%20Data%20Structures
algorithmique mathématiques
jeu. 25 oct. 2012 14:42:52 CEST -
-
link
- http://concatenative.org/wiki/view/Exotic%20Data%20Structures
algorithmique mathématiques
Math for game programmers
Une série d'articles sur les fondamentaux mathématiques pour le développement 2D/3D. On ne dirait pas comme ça, mais quand on commence à bricoler en DirectX/OpenGL, ces bases mathématiques deviennent vraiment indispensables.
ven. 13 juil. 2012 15:39:44 CEST -
-
link
- http://higherorderfun.com/blog/2009/06/07/math-for-game-programmers-01-introduction
mathématiques 3d
ven. 13 juil. 2012 15:39:44 CEST -
-
link
- http://higherorderfun.com/blog/2009/06/07/math-for-game-programmers-01-introduction
mathématiques 3d
Ce journal est basé sur Ginger, un gestionnaire de lien minimaliste développé dans le cadre d'un stage de perfectionnement. Pour plus d'informations, consulter le wiki consacré à mes projets personnels.